|
トップページ >PID制御のお話 第10回 |
|||||
| 2004年11月号 | |||||
PID制御のお話
|
|||||
| ワイド制御技術研究所 所長 広 井 和 男 |
|||||
前回、1次遅れフィルタを全PID演算の入力に、あるいは微分演算だけの入力に入れて、制御量に含まれている高周波成分を抑制して、実用形態にする工夫について説明しました。今回はその効果などを探ってみましょう。
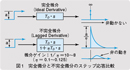
(1) 微分ゲインが1/ηとなり、入力に対する出力の上限を有限値として設定できます(ここに、η=T(一次遅れフィルタの時定数)/TD(微分時間)であり、ηの値は通常0.1~0.125で、微分ゲイン1/ηは 10~8 となる)。 (2) 入力のステップ状変化に対して、微分面積が生じて操作端を実際に動かすことができるため、微分動作が有効に働きます。 このように、不完全微分は実用上すぐれた特性をもっており、実際に多用されているにもかかわらず、日本語呼称では微分の前に「不完全」という言葉が付加されているため、しばしば誤解されてしまいます。「完全微分があるのに、なぜわざわざ不完全微分を使用するのか?」という質問を受けることがよくあります。このような誤解を避けるために、「不完全微分」のことを「実用微分」と呼んだ方が実態に合うと考えますが、皆さんのご意見はいかがでしょうか?
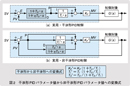
現用の制御方式である干渉形PIDの伝達関数C(s )は(1)式で表されます。 置き換える新しい非干渉形PIDの伝達関数C '(s)を(2)式で表します。 ここで(1)式を変形して、(3)式を得ます。 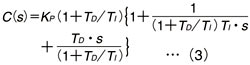 (2)式と(3)式から、干渉形PIDから非干渉PIDへの変換式は(4)式になります。 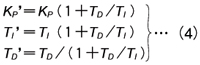 (4)式から次のことがいえます。 (1)TD=0 のとき:変換は不要で、そのまま設定すればよい。 (2)TD≠0 のとき:変換が必要〔(4)式による〕 以上の結果をまとめて、実際のPIDパラメータ値の変換法を図2に示します。
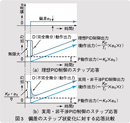
これまで説明してきたように、制御動作にはP(比例)動作、I(積分)動作およびD(微分)動作という3つの機能があり、これらを加算合成した動作をPID動作といいます。また、PID動作に基づく制御方式をPID制御と呼んでいます。 ここで、偏差がステップ状に変化したとき、理想PID制御と実用PID制御の操作出力がそれぞれどのような応答を示し、どこが異なるか明確にしておきます。 図3(a)に、ステップ偏差e 0を与えた場合の理想PID制御における出力の応答を示します。理想PID制御出力は、P動作出力とI動作出力と完全微分動作出力とを加算合成したものとなっています。一方、図3(b)には、ステップ偏差e 0を与えた場合の実用・非干渉形PID制御における出力を示します。実用・非干渉形PID制御出力は、P動作出力とI動作出力と不完全微分動作出力とを加算合成したものとなっています。この両者の応答を比較すると、P動作とI動作の出力はまったく同一であるが、D動作出力について完全微分か、不完全微分かの相違があります。完全微分の場合には、図3(a)に示すように入力ステップ状変化時の微分出力が線状になり、調節弁などの操作端にエネルギーを与えることができないため、操作端を動かすことができず、微分機能を発揮できません。不完全微分の場合には、図3(b)に示すように入力ステップ状変化時の微分出力が面積をもつので、操作端にエネルギーを与えることができて操作端が応動し、微分機能を発揮させることができます。さらに完全微分のステップ応答出力の大きさは無限大となり、高周波成分を過度に増幅して制御系を不安定にしてしまいます。これに対して、不完全微分のステップ応答出力の最高値はKP ・e 0/η(η=0.1~0.125)という有限値に抑制されるため、高周波ノイズを含む入力に対する安定性が大きく改善されることになります。 これらの2つの改善点、すなわち微分機能を発揮できることと高周波ノイズを含む入力に対する安定性の改善が、この実用形態で採用している工夫の大きな効果です。■ ◆ 参考文献 ◆ 1)宮崎 誠一:「ディジタル制御系の設計と改善」、p. 41、工業技術社(1989) |
|
||||
|
|||||