|
トップページ >PID制御のお話 第9回 |
|||||
| 2004年10月号 | |||||
PID制御のお話
|
|||||
| ワイド制御技術研究所 所長 広 井 和 男 |
|||||
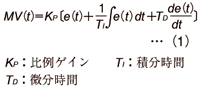 これは、いわゆる時間微分方程式であり、これを直接解くことは容易なことではありません。そこで、この時間微分方程式を時間t の領域で解く代わりに、d/dt ≡ s、∫dt ≡1/s とおいてs 領域に変換して解くのがラプラス変換法です。 この方法によると、ラプラス変換の表を参照して簡単にプロセス方程式の解が得られるだけでなく、系の特性を伝達関数によって表現でき、代数的な演算処理のみで制御系の挙動を一般的に論じることができるという大きな特長があります。 時間微分方程式をラプラス変換するには、時間の関数 f(t )をs の関数 F(s )に置き換えなければなりません。このことを、関数f(t )を時間領域(time domain)〔t 〕から s 領域(s-domain)〔s 〕の関数F(s)にラプラス変換したといい、この対応をF(s )=L[f(t )]と表現します。また、f(t )を原関数、F(s )を像関数といいます。像関数F(s )から原関数f(t )を求める変換を逆ラプラス変換(inverse Laplace transformation)といい、これを f(t )=L-1[F(s )]と表現します。例として、(1)式の時間微分方程式をラプラス変換します。E(s )=L[e(t )]、MV(s)=L[MV(t )] とおいて、(1)式をラプラス変換して整理すると(2)式を得ます。 入、出力変数の比をC(s )とすると、C(s )は(3)式で求められます。 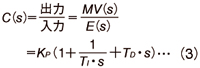 上記のようにラプラス演算子s を含んだ項をMV(s ) の係数としてくくり出すことができ、入力と出力の関係、つまりMV(s )/E(s )を計算することができます。これが微分方程式をラプラス変換して取扱う大きなメリットです。 このようにして得られた入、出力変数の比C(s )をPID制御の伝達関数(transfer function)と呼びます。系の入力E(s ) が分かれば、出力はMV(s )=C(s )・E(s ) として求めることができるので、系の特性は伝達関数C(s)で表すことができます。伝達関数が分かると、入力e(t)が入ったときの系の応答MV(t )は逆ラプラス変換をして(4)式のようにして求めることができます。 具体的には、ラプラス変換表を逆に引いて求めることができます。
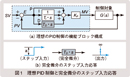
この理想PID制御は微分項が「完全微分」(TD・s )で構成されているのが特徴です。 このため、圧力、流量、レベル、温度や成分などの制御量の計測信号に重畳している高周波ノイズが完全微分によって過度に増幅拡大されて、制御系を不安定にするという問題があります。さらに図1(b)に示すように、偏差のステップ変化に対する完全微分の出力波形は線状となり、操作端にエネルギーを与えることができず、操作端が動かないため、実際に微分動作をしないという問題もあります。
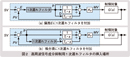
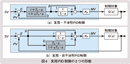
この1次遅れフィルタの入れ方には図2(a)、(b)に示す2通りの方法があります。 3. 1 具体的1次遅れフィルタの形式 図3に示すように、挿入する1次遅れフィルタの時定数をT =η・TD[TD:微分時間、η:微分係数(通常0.1~0.125、 1/η=8~10)]とすると、1次遅れフィルタの伝達関数は(5)式となります 。 3. 2 実用PID制御の伝達関数 高周波信号成分抑制用1次遅れフィルタの挿入場所によって、実用PID制御の伝達関数は2種類のものが生まれます。 3. 2. 1 実用・干渉形PID制御 (5)式で表される1次遅れフィルタを図2(a)に示す位置に入れて、PID制御演算に入る偏差信号Eに含まれる高周波成分を抑制するようにした構成におけるPID制御伝達関数C(s )を近似計算して求めると、(6)式となります。 (6)式は微分時間TD ≠ 0のとき、つまり微分動作が存在するときには、D動作がP動作およびI動作に影響を与えることから「実用・干渉形PID制御」と呼ばれています。この機能ブロック構成を図4(a)に示します。 3. 2. 2 実用・非干渉形PID制御 (5)式で表される1次遅れフィルタを図2(b)に示すように微分項だけの入力側に入れて、D動作に入る偏差信号Eに、含まれる高周波成分を抑制するようにした構成におけるPID制御伝達関数C(s )を求めると、(7)式となります。 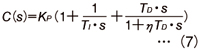 (7)式はPID制御の各動作が完全に独立しており、他に影響を及ぼさないことから「実用・非干渉形PID制御」と呼ばれています。この機能ブロック構成を図4(b)に示します。この形態のPID制御は非常に多く使用されています。■ |
|
||||
|
|||||