|
トップページ >PID制御のお話 第8回 |
||||||
| 2004年9月号 | ||||||
PID制御のお話
|
||||||
| ワイド制御技術研究所 所長 広 井 和 男 |
||||||
| ここで、P(比例)I(積分)制御は制御という視点から見て完全なものか、それとも何か欠けているものがあるかを、人間が制御するときの考え方と対比しながら考察してみましょう。 人間が物事を判断するときには、(1)「過去」はどのようになっていたか?、(2)「現在」はどのようになっているか?、(3)「将来」はどのようになりそうか?という、過去、現在および将来の3つの情報を利用し、問題の性質によってそれぞれに重みをつけて的確な結論を出すように努めています。P制御は「現在の偏差」の大きさに比例した修正出力を出し、I制御は「過去の偏差」の積分(累積値)の大きさに比例した修正出力を出していることになります。人間の制御思考と比べてみると、PI制御には「将来の偏差」に関する情報を活用する成分が欠けています。
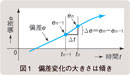
偏差e の将来動向を予測して、その変化を抑制するように制御するためには、現在の偏差の変化速度Δy に比例した修正出力を活用すればよいことになります。つまり(2)式に示すように、偏差e の微分値に比例した修正出力を使用すればよいことになります。  この(2)式は、いわゆる微分(D:Derivative)制御と呼ばれているものです。D制御出力MVD は、偏差e が変化しているときには変化速度に比例した修正出力を出しますが、偏差e が時間的に変化していないときにはゼロになります。たとえば、偏差e が一定速度で変化していく場合には、D制御出力MVD はその変化速度に比例した一定値になります。つまり、偏差e の変化速度が大きいほど、出力は大きくなります。したがって、D制御にはフィードバック制御系の制御応答の動特性を改善する働きがあります。 D制御もI制御と同様に単独で使用されることはなく、P制御あるいはPI制御と組み合わせて、PD制御あるいはPID制御として使用されます。
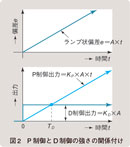
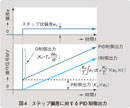
KP : 比例ゲイン KD : 微分ゲイン (3)式の比例ゲイン KP と微分ゲイン KD の強さを関係付けるものとして、図2に示すように、ランプ状偏差が入ったときD制御出力がP制御出力と同じ値になるまでの時間を微分時間TD(Derivative time)と定義しています。 A :ランプ状偏差の比例係数 ここで(4)式=(5)式として、KD を求めると(6)式になります。 (6)式を(3)式に代入すると、(7)式を得ます。(7)式が、いわゆる「PD制御式」です。 この(7)式に積分(I)制御(本連載第6回、本誌2004年7月号参照)を付加したPID制御式は(8)式となります。 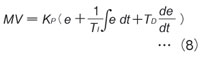 KP :比例ゲイン TI :積分時間 TD :微分時間 これがPID制御基本式です。各項を導出するときに説明したように、P制御は「現在の偏差」の大きさに、I制御は「過去の偏差」の累積値に、D制御は「将来の偏差」の予測値(偏差の変化速度)に、それぞれ重みを付けて加算し、PID制御出力にしています。
しかし、比例ゲインKP を大きくし過ぎると制御応答が振動的となるので、KP の大きさには限界があり、P制御のみではオフセットが残ってしまいます。 そこでI制御を付加してPI制御にすると、I制御機能によって偏差がある限り偏差をゼロにしようとして操作信号を変化し続けるため、定常状態で偏差はゼロとなってオフセットがなくなり、PI制御では制御量を目標値にピッタリ一致させることができます。さらに偏差の変化速度を用いて予測制御する機能をもつD制御を付加したPID制御では、偏差発生から定常状態に至るまでの過渡応答特性を改善することができます。■ |
|
|||||
|
||||||