エムエスツデー　2003年2月号

交流の測定

正弦波交流の大きさの表現法

正弦波交流f（t）の大きさを示す様々な表現方法を以下に列挙します（併せて図1もご参照ください）。

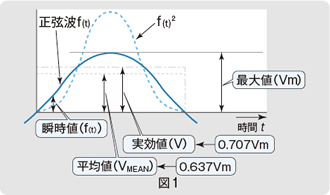
　1）瞬時値［f（t）］ ：任意の瞬間における値
　2）最大値［Vm］ 　：瞬時値における最も大きい値
　3）平均値［VMEAN］ ：瞬時値の絶対値を1周期（T）について平均した値

平均値を数式で表すと、式（1）となります。

　4）実効値［V］ ：瞬時値の二乗平均の平方根

実効値を数式で表すと、式（2）となります。

ちょっと複雑ですが、実効値とは、直流と同じ大きさの電力が得られる交流の大きさを、その直流の大きさで表したものであり、具体的な例で言えば、抵抗負荷に、ある大きさの交流を流したときと直流を流したときに発生する電力（熱量）が同じである場合、その直流の値（電圧または電流値）をもってその交流の「実効値」として表すものであって、とくに断らない限り、交流の大きさは実効値で表現するのが一般です。

交流の測定

交流を取り扱う場合には、ほとんどの場合実効値が必要になります。昔は、交流には主トランスの励磁電流やコンデンサの充電電流などに基づく、わずかな波形歪みしかないきれいな波形の交流でした。したがって、平均値演算を行ったメータに実効値目盛りを付ける（1.111倍にする）ことによって実効値を表示していました。このメータが「可動コイル形メータ」になります。特長としては、一般に目盛りが均等割りになっている点です。一方、波形歪みが多く存在する交流の測定には「可動鉄片形メータ」が使用されていました。このメータは実効値演算が行え、特長としては、一般に不均等割りの目盛りになっています。

現在市販されている交流変換器についても、同じように数種類の演算方式が採用されています。電力を便利かつ効率よく使用しようとしている現在では、コンバータ、インバータなどが多数使用されており、電力配線における交流波形の予測はかなり困難なことだと思いますから、一般に、「実効値演算方式」の変換器の使用を推奨します。

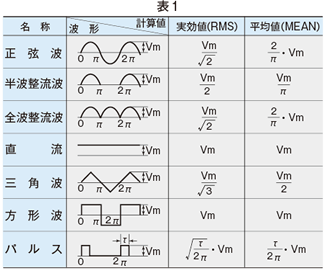
各種波形の実効値と平均値

参考として、表1に代表的な波形とその実効値、平均値を掲載します。

【（株）エム･システム技研　開発部】